Answer:
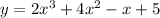
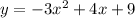
Explanation:
The given equation is in the form

We have to evaluate the correct system of equations which can be used to find the roots of the equation.
We can find the root of the equation by plotting the graph of the equations. In order to graph, we can assume the left and right hand side of the given equation as two separate equations.
Therefore, we have
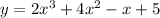
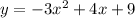
Now, we plot the graph of these two equations in the same coordinate plane. The intersection point (s) would be the roots of the given equation.
Hence, the system of equation that we can use to find the root of the given equation is
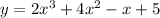
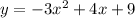
Last option is correct.