Question

Factor f(x) = 4x² + 28x + 48

Answer 1

4(x + 3)(x + 4)

Step-by-step explanation

We want to factorise:

4x² + 28x + 48​

We simply want to write the expression as a product of its factors.

First, because each of the coefficients in the expression and the constant are divisible by 4, we will factor out 4:

`4(x^2\text{ + 7x + 12)}`

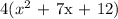
Now, we have to look for two numbers such that adding them will yield 7 and their product will yield 12.

The two numbers we need are:

3 and 4

So, we have that the expression becomes:

`\begin{gathered} 4(x^2\text{ + 3x + 4x + 12)} \\ \Rightarrow\text{ 4\lbrack{}x(x + 3) + 4(x + 3)\rbrack} \\ \Rightarrow\text{ 4(x + 3)(x + 4)} \end{gathered}`

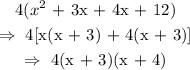
We have factorised it.