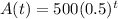Question

the half life of a medication is the time it takes for the medication to reduce to half of its original amount in a patient's bloodstream. A certain antibiotic has a half-life of about 8 hours. a patient is administrated 500 miligrams of the medication. Write a function that models the amount of the medication in the patients bloodstream over time

Answer 1

R=S*0.5^(t/8)
R is the remaining amount
S is the starting amount (500)
0.5^ is for the HALF in half-life
t/8 show that every 8 ts (every 8 hours), it will be halved once
...so plug in 500mg for the general solution...
R=(500)*(0.5)^(t/8)
... plug in 24h to solve for after 24h
R=(500)*(0.5)^(24/8)
R=(500)*(0.5)^(3)
R=(500)*(0.125)
R=(0.0625)
...therefore there with be 0.0625 mg of the dose remaining

Answer 2

`A(t)=500(0.5)^(t)`

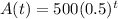
Explanation:

Half life of an antibiotic is 8 hours so the sequence formed at every 8 hours showing the amount of drug in the blood stream will be

Time 0 8 16 32

Concentration in blood 500 250 125 62.5

(in mg)

We can see from the table that the sequence formed is geometric in nature.

So the explicit formula for this sequence will be

`A_(t)=A_(0)(r)^(t)`

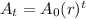
Where
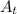`A_(t)` = Amount of drug in the blood after time t hours

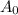`A_(0)` = Loading dose

r = Common ratio of the sequence

t = time or duration

From this sequence r =
`(250)/(500)=0.5`

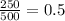
Therefore, the explicit formula will be

`A_(t)=500(0.5)^(t)`

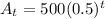
We can rewrite the formula in the form a function

`A(t)=500(0.5)^(t)`