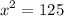
![\begin{gathered} \sqrt[]{x^2}=\sqrt[]{125} \\ \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/vk0ajg0u8lwusuyxg9t8.png)
Every positive number has two square roots, one positive and one negative:
![\begin{gathered} \sqrt[]{a^2}=\pm a \\ \\ \text{Because:} \\ a\cdot a=a^2 \\ (-a)\cdot(-a)=a^2 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/g5ebwoa7wn1gzqde4u08.png)
For solving the given expression, as 125 is not a perfect square the solution for x is both a negative and a positive:
![\begin{gathered} x=\pm\sqrt[]{125} \\ \\ x=\sqrt[]{125} \\ x=-\sqrt[]{125} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/7m3hbmsg2wioxdtm7raf.png)
To know when do you assign a +/- to the answer you use the contex of the equation, e.g: if x is a distance it can not be negative so the solution is the positive one.
You can also simplify the square root of 125 as follow:
Prime factorization of 125:
![\begin{gathered} 125=5\cdot5\cdot5=5\cdot5^2 \\ \\ x=5(\pm\sqrt[]{5}) \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/666pimnt57vjb52pppef.png)