Question

A theater has 10 seats in the first row and 30 seats in the 6th row.A. How many seats are in the 11th row B. The theater has a total of 21 rows. How many total seats are there

Answer 1

(a)14 seats

(b)1,050 seats

Step-by-step explanation:

The theater has 10 seats in the first row and 30 seats in the 6th row.

We can model this as an arithmetic progression problem where:

• The first term, a = 10

,

• The last term, l = 30 when n=6

We know that for an arithmetic progression:

`\begin{gathered} l=a+(n-1)d \\ 30=10+(6-1)d \\ 30=10+5d \\ 5d=30-10 \\ 5d=20 \\ d=(20)/(5)=4 \end{gathered}`

Therefore, the number of seats in the 11th row will be:

`a_(11)=10+4=14\text{ seats}`

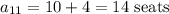
(b)The theater has a total of 21 rows.

To determine the total number of seats, we use the formula for the sum of an arithmetic progression.

`S_n=(n)/(2)(2a+(n-1)d)`

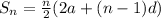
We define the variables:

• Since the theatre has a total of 21 rows, therefore n=21

,

• The first term, a = 10

,

• Common difference, d = 4

We substitute into the formula above:

`\begin{gathered} S_n=(n)/(2)(2a+(n-1)d)\implies S_(21)=(21)/(2)(2*10+(21-1)*4) \\ =10.5(20+20*4) \\ =10.5(20+80) \\ =10.5*100 \\ =1050 \end{gathered}`

There are a total of 1,050 seats in the theater.