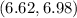Step-by-step explanation:
The given values in the question are
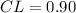
We will forst of all calculate the margin of error using the formula below
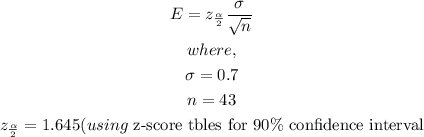
Hence,
The margin of erro will be
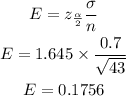
Hence,
The lower limit and upper limit will be calculated using the formula below
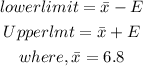
By substituitng the values, we will have
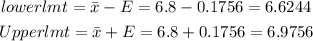
Hence,
The final answers to to decimal places is given below as