Question

credit. 1. In this problem, we are going to verify that Heron's Formula works for a right triangle. I am going to use a 3,4,5 Right Triangle. The Pythagorean Theorem (A squared plus B squared equals C squared) or The A = 3 B = 4 and the hypotenuse (or third side, always the longest side) C is 5 so evaluating 3^2 + 4^2 = 5^2 or 9 + 16 = 25 and 25 = 5^2 = 25. It does! Therefore a 3,4,5 triangle is a right triangle. Using A = bh/2 or the b = 3 and h = 4 or 3*4/ 2 or 12/2 = 6. I leave it for you to use Heron's Formula to verify you get the same answer. This is the first question and to do it, you follow the procedure above. - Step 1:1 Step 2: Step 3: Step 4: Step 5: Step 6: 2. By the use of the Pythagorean Theorem show that a 3, 4, 5 sided ngle is a right triangle. The C side is always the longest side. 3. Now that you have used the Pythagorean Theorem, show that a 5, 12, 13 is a right triangle. Then find the area both ways, A = bh/2 and using Heron's Formula.

Answer 1

1.

We need to use Heron's formula to verify that we get the same area.

Heron's formula is given as:

`A=\sqrt[]{s(s-a)(s-b)(s-c)}`

where:

`s=(a+b+c)/(2)`

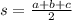
In this case we have that a=3, b=4 and c=5. Then:

Step 1: Find s

`s=(3+4+5)/(2)=6`

Step 2: Find s-a

`s-a=6-3=3`

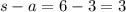
Step 3: Find s-b

`s-b=6-4=2`

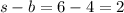
Step 4: Find s-c

`s-c=6-5=1`

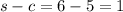
Step 5: Plug the values in Heron's formula

`\begin{gathered} A=\sqrt[]{6\cdot3\cdot2\cdot1} \\ A=\sqrt[]{36} \\ A=6 \end{gathered}`

Step 6: Verify that it is the same area

We notice that the area using A=1/2bh and Heron's formula is the same.

2.

Triangle 3, 4, 5 is a right triangle. to prove we use the pythagorean theorem:

`c^2=a^2+b^2`

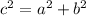
If we choose a=3, b=4 and c=5 then:

`\begin{gathered} 5^2=3^2+4^2 \\ 25=9+16 \\ 25=25 \end{gathered}`

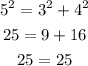
since the pythagorean theorem holds we conclude that the triangle is a right one.

3.

Now we have a triangle with sides 5, 12 and 13 and we need to prove that this is a right triangle. We are going to use the pythagorean theorem to prove it choosing a=5, b=12 and c=13, we have that:

`\begin{gathered} 13^2=5^2+12^2 \\ 169=25+144 \\ 169=169 \end{gathered}`

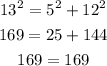
Since the pythagorean theorem holds we conclude that the triangle with sides 5, 12 and 13 is right triangle.

Now we need to find the area with the formula:

`A=(1)/(2)bh`

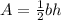
in this case we have:

`A=(1)/(2)(5)(12)=30`

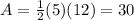
therefore the area is 30 squared units.

Finally we use Heron's formula:

`A=\sqrt[]{s(s-a)(s-b)(s-c)}`

In this case we have that:

`s=(5+12+13)/(2)=15`

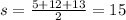
then:

`\begin{gathered} s-a=15-5=10 \\ s-b=15-12=3 \\ s-c=15-13=2 \end{gathered}`

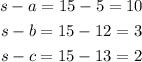
Plugging the values in the formula we have:

`\begin{gathered} A=\sqrt[]{15\cdot10\cdot3\cdot2} \\ A=\sqrt[]{900} \\ A=30 \end{gathered}`

Therefore the area is 30 squared units and we get the same result.