Question

I was getting help on this earlier but my tutor got disconnected.Celeste walked 147 ft on a moving walkway at the airport. Then she walked on the ground for 98ft She travels 2/ftsec faster on the walkway than she does on the ground. If the time it takes her to travel the total distance of 245ft is 49sec, how fast does Celeste travel on and off the moving walkway?

Answer 1

Let x be the walking in the ground speed; since she travels 2 ft/s faster on the walkway its velocity there is:

`x+2`

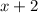
Now we know that she traveled 147 ft on the walkway and in total 245 ft, this means that she traveled 98 ft on the ground.

We also know that the speed is given as:

`v=(d)/(t)`

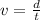
from this the time is:

`t=(d)/(v)`

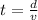
The time she spent on the walkway is:

`t=(147)/(x+2)`

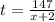
while the time she walked on the ground is:

`t^(\prime)=(98)/(x)`

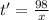
Now, adding this times and equating them to the total time she walked we get:

`(147)/(x+2)+(98)/(x)=49`

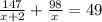
Solving for x we have:

`\begin{gathered} (147)/(x+2)+(98)/(x)=49 \\ (147x+98(x+2))/(x(x+2))=49 \\ (147x+98x+196)/(x^2+2x)=49 \\ 245x+196=49(x^2+2x) \\ 245x+196=49x^2+98x \\ 49x^2-147x-196=0 \\ x^2-3x-4=0 \\ (x+1)(x-4)=0 \\ \text{then} \\ x=-1 \\ \text{ or} \\ x=4 \end{gathered}`

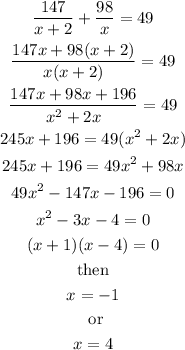
Now, since she walked in the same direction the velocity can't be negative.

Therefore we conclude that the ground speed was 4 ft/s while the walkway speed was 6 ft/s.