Question

Consider a sequence defined by the explicit rule f(n)=-8+3 (n − 1). Choose True or False for each statement.

Answer 1

Given the general n th term of the sequence,

`f(n)=-8+3(n-1)`

For n = 1,

`\begin{gathered} f(1)=-8+3(1-1) \\ =-8 \end{gathered}`

Therefore, the first statement is true.

Now for n = 2,

`\begin{gathered} f(2)=-8+3(2-1) \\ =-8+3 \\ =-5 \end{gathered}`

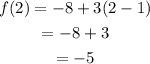
Therefore, the first two terms of the sequence is -8 and -5.

So, the common difference is,

`-5-(-8)=-5+8=3`

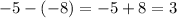
Therefore, the common difference is 3.

So, the second statement is true.

Now fifth term is for n = 5.

Therefore,

`\begin{gathered} f(5)=-8+3(5-1) \\ =-8+(3*4) \\ =-8+12 \\ =4 \end{gathered}`

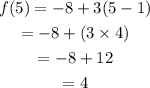
Therefore the fifth term is 4 but not 7.

Hence, the third statement is false.