Question

Using the Converse of Basic Proportionality Theorem Explain why the following pairs are parallelPQ and NM

Answer 1

The Converse of Basic Proportionality Theorem states that if a line divides any two sides of a triangle in the same ratio, then the line must be parallel to the third side.

Find the ratio of the segments in which the line PQ divides the segments LM and LN. If the ratio is the same, then by the above mentioned theorem, we could conclude that PQ and NM are parallel.

Notice that the point P divides the segment LN into segments LP and PN. The ratio of LP to LN is:

`(LP)/(LN)=(9)/(75)=(9/3)/(75/3)=(3)/(25)`

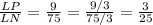
Notice that the point Q divides the segment LM into segments LQ and QM. The ratio of LQ to LM is:

`(LQ)/(LM)=(12)/(100)=(12/4)/(100/4)=(3)/(25)`

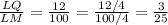
Since both ratios are the same, then:

`PQ\mleft\Vert NM\mright?`

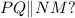
Which is a mathematical notation to state that PQ and NM are parallel.