Question

Use the point-slope form to find the equation of each altitude of SABC. (Recall ! a triangle is the perpendicular drawn from any vertex to the opposite side.) (b) A(4,3), B(0,7). C- (a) A(1, -2), B(3,4), C(-2,6)

Answer 1

The rule of the slope of a line has 2 points is

`m=(y2-y1)/(x2-x1)`

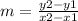
A = (1, -2), B = (3, 4), C = (-2, 6)

We will take the altitude from A to the opposite side of BC

Then we will find the slope of BC first

x1 = 3 and y1 = 4. point B

x2 = -2 and y2 = 6. point C

We will substitute them in the rule above

`\begin{gathered} m=(6-4)/(-2-3)=(2)/(-5) \\ m=-(2)/(5) \end{gathered}`

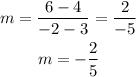
The slope of BC = -2/5

Since the product of the slopes of the perpendicular line is -1, then if the slope of one is m, then the slope of the other will be -1/m, we reciprocal it and change its sign, then the slope of the altitude of BC should be 5/2

`m_(\perp)=(5)/(2)`

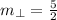
The form of the equation in point-slope is

y - y1 = m(x - x1)

m = 5/2

Since point A is lying on the altitude from A to BC, then

x1 = 1 and y1 = -2 point A

Substitute m and coordinates of point A in the form of the equation above

y - (-2) = 5/2 (x - 1)

`y+2=(5)/(2)(x-1)`

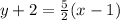
The equation of the altitude from A to BC is

y + 2 = 5/2 (x - 1)