Question

Which of the following represents the factored form of f(x) = x3 − 121x?

f(x) = (x + 11)(x − 11)
f(x) = x(x + 11)(x − 11)
f(x) = x(x − 11)2
f(x) = x(x2 − 11)

Answer 1

Hello here is a solution :
f(x) = x3 − 121x = x(x²-121) = x (x² -11²)
f(x) = x (x+11)(x-11)

Answer 2

f(x) = x (x -11) (x +11).

Explanation:

Given : f(x) = x³ − 121x

To find : factors.

Solution : We have given that f(x) = x³ − 121x

Taking common we get,

x ( x² - 121 )

By
`(a^(2) -b^(2)) =( a-b) (a+b)`.

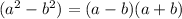Then

( x² - 11² ) = (x -11) (x +11).

Therefore, f(x) = x (x -11) (x +11).