Question

Describe the transformations to the graph of y=xthat result in the graph of y=3(x - 2)2 + 1 O A. Shift left 2 units, down 1 units, then stretch by a factor of 3 B. Shift right 2 units, stretch by a factor of 3, then shift up 1 unit O C. Shift up 2 units, down 1 units, then reflect across the x-axis O D. Stretch by a factor of 3, shift down 2 units, then up 1 unit

Answer 1

Remember the following rules for transformations of functions:

Vertical shift by c units (upwards):

`f(x)\rightarrow f(x)+c`

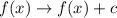
Horizontal shift by c units (towards the right):

`f(x)\rightarrow f(x-c)`

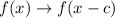
Vertical stretch by a factor c:

`f(x)\rightarrow c\cdot f(x)`

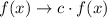
We can identify the following elements in the equation of y=3(x-1)^2+1 :

1.- Shift right 2 units.

2.- Vertical stretch by a factor of 3

3.- Shift up 1 unit.

The option that displays these transformation is option B.

Therefore, the answer is:

Option B)

Shift right 2 units, stretch by a factor of 3, then shift up 1 unit.