Question

Given the function g(x)=-x^2+6x+12, determine the average rate of change of the function over the interval −3≤x≤5.

Answer 1

Given:

`g(x)=x^2+6x+12`

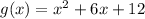
And given interval is

`[a,b]=[-3,5]`

Required:

To find the average rate of change of the given function over the interval −3≤x≤5.

Step-by-step explanation:

To calculate the average rate of change between the 2 points use.

`(g(b)-g(a))/(b-a)`

Here,

`\begin{gathered} g(b)=g(5) \\ \\ =5^2+6*5+12 \\ \\ =25+30+12 \\ \\ =67 \end{gathered}`
`\begin{gathered} g(a)=g(-3) \\ \\ =(-3)^2+6(-3)+12 \\ \\ =9-18+12 \\ \\ =3 \end{gathered}`

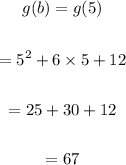
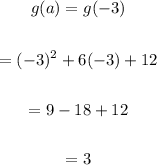
Therefore,

`\begin{gathered} (g(b)-g(a))/(b-a)=(67-3)/(5-(-3)) \\ \\ =(64)/(8) \\ \\ =8 \end{gathered}`

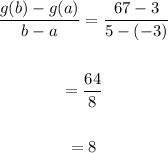
Final Answer:

The average rate of change of the function over the interval −3≤x≤5 is 8.