Question

An Individual Retirement Account (RA) has $11,000 in it, and the owner decides not to add any more money to the account other than interest earned at 3%compounded daily. How much will be in the account 38 years from now when the owner reaches retirement age?

Answer 1

`A=\$34,430`

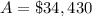
Step-by-step explanation: The principal amount of $11,000 Is deposited in an account and it is compounded on daily basis at the interest rate of 3%, the formula used to solve this problem is as follows:

`\begin{gathered} A=P(1+(r)/(n))^(n\cdot t)\Rightarrow(1) \\ P\Rightarrow\text{ Initial amount} \\ n\Rightarrow\text{ Number of times compounded per time-period} \\ r\Rightarrow\text{ Interest rate} \\ t\Rightarrow\text{ Time period} \end{gathered}`

Substituting the knowns in the formula (1) gives the answer as follows:

`\begin{gathered} A=(11000)\cdot(1+(0.03)/(365))^((365\cdot38))=(11000)\cdot(3.13)=34,430 \\ A=\$34,430 \end{gathered}`

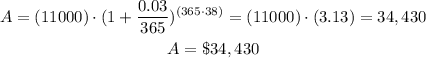
So after 38 years, the amount in the account will be $34,430.