To find the mean of grouped data, we need to use the next formula:
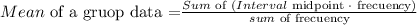
First, we need to find the midpoint of each interval:
The midpoint of interval = 1/2 (lower class limit + upper-class limit)
Then:
Time for competition (in minutes) ----- frequency ---- midpoint
9 -11 8 1/2(9+11) = 10
12 -14 7 1/2(12+14) = 13
15-17 5 1/2(15+17)= 16
18 - 20 3 1/2(18+20) = 19
21-23 3 1/2(21+23) = 22
Now, multiply the frequency of each interval by its midpoint:
10 * 8 = 80
13* 7 = 91
16 * 5 = 80
19 * 3 = 57
22 *3 = 66
Summ all the results 80 + 91 +80+57+66= 374
Then, sum all the frecuencys = 8 + 7 +5 +3 +3 = 26
Use the mean formula =
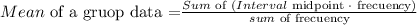
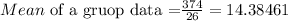
The mean is given using five decimals.