Question

Given the following sequences: I. 2,4,6,8,10... II.2,4,8,16,32... III. a,a + 2, a + 4, a + 6, a +8... Which ones are arithmetic sequences?

Answer 1

The arithmetic sequences are: I and iii

Step-by-step explanation

The formula for the nth term of an arithmetic sequence is:

`a_n=a_1+d(n-1)`

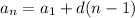
where a1 is the first term of the sequence and d is the common difference.

For the first sequence I. 2, 4, 6, 8, 10... we can find the common difference by subtracting the first term from the second:

`\begin{gathered} a_2=a_1+d(2-1) \\ a_2=a_1+d \\ d=a_2-a_1 \\ d=4-2 \\ d=2 \end{gathered}`

So the nth term of this sequence is:

`a_n=2+2(n-1)`

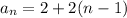
Each term of this sequence follows this rule. Therefore this is an arithmetic sequence.

For the second sequence II. 2, 4, 8, 16, 32... there's no common difference because between the first and second term there's a difference of 2, between the second and third there's a difference of 4, and this increases as we move through the sequence. Therefore this is not an arithmetic sequence.

For the third one, III. a, a+2, a+4, a+6, a+8... we can see that there is a common difference:

`\begin{gathered} a_2_{}_{}=a_1+d(2-1) \\ d=a_2-a_1 \\ d=a+2-a \\ d=2 \end{gathered}`

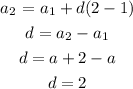
The rule for the nth term is:

`a_n=a+2(n-1)`

Let's find the first 5 terms:

`\begin{gathered} a_1=a+2(1-1)=a \\ a_2=a+2(2-1)=a+2 \\ a_3=a+2(3-1)=a+4 \\ a_4=a+2(4-1)=a+6 \\ a_5=a+2(5-1)=a+8 \end{gathered}`

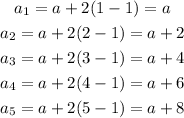
This shows that each term follows the same rule. Therefore this is an arithmetic sequence.