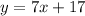Question

Consider the line y=7x-1Find the equation of the line that is perpendicular to this line and passes through the point −2, 3.Find the equation of the line that is parallel to this line and passes through the point −2, 3.Note that the ALEKS graphing calculator may be helpful in checking your answer.Equation of per pendicular line:Equation of parallel line:

Answer 1

Step-by-step explanation

Algebra / Graphs and Functions / Equations of Parallel and Perpendicular Lines

We have the line:

`y=7x-1.`

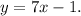
We must find the equation:

0. of the perpendicular line,

,

1. and the parallel line,

to the given line that passes through the point (-2, 3).

1) Perpendicular line

The equation of the perpendicular line has the form:

`y=m_p\cdot(x-x_0)+y_0.`

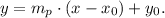
Where mₚ is the slope, and (x₀, y₀) = (-2, 3).

From the equation of the given line, we see that its slope is m = 7. The slope of the perpendicular line mₚ is given by the equation:

`\begin{gathered} m\cdot m_p=-1, \\ 7\cdot m_p=-1, \\ m_p=-(1)/(7). \end{gathered}`

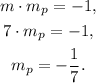
Replacing mₚ = -1/7 and (x₀, y₀) = (-2, 3) in the equation of the perpendicular line, we get:

`y=-(1)/(7)\cdot(x-(-2))+3=-(1)/(7)\cdot(x+2)+3=-(1)/(7)\cdot x-(2)/(7)+3=-(1)/(7)\cdot x+(19)/(7).`

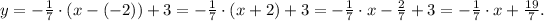
2) Parallel line

The equation of the perpendicular line has the form:

`y=m_p\cdot(x-x_0)+y_0.`

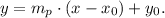
Where mₚ is the slope, and (x₀, y₀) = (-2, 3).

From the equation of the given line, we see that its slope is m = 7. The parallel line has the same slope as the given line, so we have:

`\begin{gathered} m_p=m, \\ m_p=7. \end{gathered}`

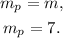
Replacing mₚ = 7 and (x₀, y₀) = (-2, 3) in the equation of the parallel line, we get:

`y=7\cdot(x-(-2))+3=7\cdot(x+2)+3=7x+14+3=7x+17.`

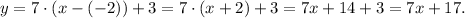
3) Graph

Plotting the equations obtained, we get the following graph:

Answer

1) Equation of the perpendicular line:

`y=-(x)/(7)+(19)/(7)`

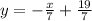
2) Equation of the parallel line:

`y=7x+17`