Question

(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.) And determine the quadrants of A+B and A-B.

Answer 1

Given that:

`\cos A=(5)/(13)`

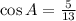
Where:

`0And:[tex]\cos B=(3)/(5)`

Where:

Therefore, applying this formula, you can find the measure of angles A and B:

`A=\cos ^(-1)((5)/(13))\approx67.38\text{\degree}`
`B=\cos ^(-1)((3)/(5))\approx53.13\text{\degree}`

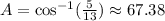
(a) By definition:

`\sin \mleft(A+B\mright)=sinAcosB+cosAsinB`

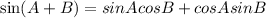
Knowing that:

`\sin \theta=(opposite)/(hypotenuse)`

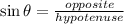
You can substitute the known values into the equation in order to find the opposite side for angle A:

`\begin{gathered} \sin (67.38\text{\degree)}=(opposite)/(13) \\ \\ 13\cdot\sin (67.38\text{\degree)}=opposite \\ \\ opposite\approx12 \end{gathered}`

Now you know that:

`\sin A=(12)/(13)`

Using the same reasoning for angle B, you get:

`\begin{gathered} \sin (53.13\text{\degree)}=(opposite)/(5) \\ \\ 5\cdot\sin (53.13\text{\degree)}=opposite \\ \\ opposite\approx4 \end{gathered}`

Now you know that:

`\sin B=(4)/(5)`

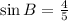
Substitute values into the Trigonometric Identity:

`\begin{gathered} \sin (A+B)=sinAcosB+cosAsinB \\ \\ \sin (A+B)=((12)/(13))((3)/(5))+((5)/(13))((4)/(5)) \end{gathered}`

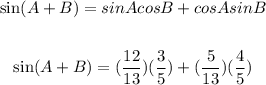
Simplifying, you get:

`\begin{gathered} \sin (A+B)=(36)/(65)+(20)/(65) \\ \\ \sin (A+B)=(36+20)/(65) \end{gathered}`
`\sin (A+B)=(56)/(65)`

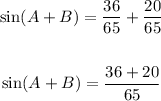
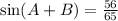
(b) By definition:

`\sin \mleft(A-B\mright)=sinAcosB-cosAsinB`

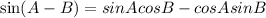
Knowing all the values, you get:

`\begin{gathered} \sin (A-B)=((12)/(13))((3)/(5))-((5)/(13))((4)/(5)) \\ \\ \sin (A-B)=(36-20)/(65) \\ \\ \sin (A-B)=(16)/(65) \end{gathered}`

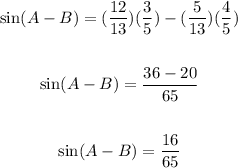
(c) By definition:

`\tan (A+B)=(\tan A+\tan B)/(1-\tan A\cdot\tan B)`

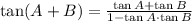
By definition:

`\tan \theta=(opposite)/(adjacent)`

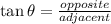
Therefore, in this case:

- For angle A:

`\tan A=(12)/(5)`

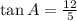
- And for angle B:

`\tan B=(4)/(3)`

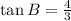
Therefore, you can substitute values into the formula and simplify:

`\tan (A+B)=((12)/(5)+(4)/(3))/(1-((12)/(5)\cdot(4)/(3)))`
`\tan (A+B)=((56)/(15))/(1-(48)/(15))`
`\tan (A+B)=((56)/(15))/(-(11)/(5))`
`\tan (A+B)=-(56)/(33)`

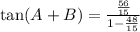
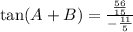
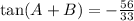
(d) By definition:

`\tan (A-B)=(\tan A-\tan B)/(1+\tan A\cdot\tan B)`

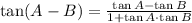
Knowing all the values, you can substitute and simplify:

`\tan (A-B)=((12)/(5)-(4)/(3))/(1+((12)/(5)\cdot(4)/(3)))`
`\tan (A-B)=((16)/(15))/((21)/(5))`
`\tan (A-B)=(16)/(63)`

(e) Knowing that:

`\sin (A+B)=(56)/(65)`
`\tan (A+B)=-(56)/(33)`

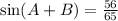
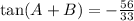
Remember the Quadrants:

By definition, in Quadrant II the Sine is positive and the Tangent is negative.

Since in this case, you found that the Sine is positive and the Tangent negative, you can determine that this angle is in the Quadrant II:

`A+B`