Question

Consider the graph of g(x) shown below. Determine which statements about the graph are true. Select all that apply.

Answer 1

From the graph, the root of the equation is the point where the graph touches the x-axis

`x=-4,x=0`

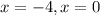
Hence the equation that models the graph becomes

`\begin{gathered} x+4=0,x-0=0 \\ x(x+4)=0 \\ x^2+4x=0 \\ \text{Hence } \\ g(x)=x^2+4x \end{gathered}`

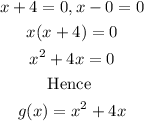
Since the solution to the equation are x=-4 and x=0

Hence the equation has two real zeros

The minimum of g(x) is at the point

`\begin{gathered} (-2,-4) \\ \text{Hence minimum is at x=-2} \end{gathered}`

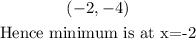
The minimum of g(x) is at x=-2

The vertex of g(x) is given by

`\begin{gathered} x_v=-(b)/(2a) \\ \text{and substistitute into the equation to get } \\ y_v \end{gathered}`
`\begin{gathered} a=1,\: b=4,\: c=0 \\ x_v=-(b)/(2a)=-(4)/(2*1)=-(4)/(2)=-2 \\ y_v=x^2+4x=(-2)^2+4(-2)=4-8=-4 \\ \text{vertex (-2,-4)} \end{gathered}`

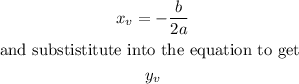
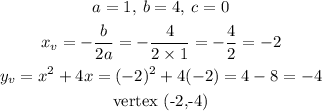
Hence the vertex of g(x) is (-2,-4)

The domain of the function g(x) is the set of input values for which the function g(x) is real or define

Since there is no domain constrain for g(x), the domain of g(x) is

`(-\infty,\infty)`

hence the domain of g(x) is (-∞,∞)

The decreasing function the y-value decreases as the x-value increases: For a function y=f(x): when x1 < x2 then f(x1) ≥ f(x2)

Hence g(x) decreasing over the interval (-∞,-2)

Therefore for the graph above the following apply

g(x) has two real zeros (option 2)

The minimum of g(x) is at x= - 2(option 3)

the domain of g(x) is (-∞,∞) (option 4)

g(x) decreasing over the interval (-∞,-2)(option 4)