Question

Give the point-slope form of the equation of the line that is perpendicular to y= -4x/5+10 and contains P(5,6)

Answer 1

You have to write the equation of a line perpendicular to

`y=-(4)/(5)x+10`

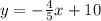
That crosses the point (5, 6)

A caracteristic of a line permendicular to another one is that its slope pf the perpendicular line is the negative inverse of the slope of the first line.

So for example if you have two lines:

1_ y=mx+b

and

2_ y=nx+c

And both lines are perpendicular, the slope of the second one will be the negative inverse of the slope of the first one, that is:

`n=-(1)/(m)`

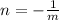
The slope of the given line is m=-4/5

The negative inverse is

`-((1)/(-(4)/(5)))=-(-(5)/(4))=(5)/(4)`

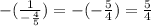
Now that you know the slope of the perpendicular line, use it along with the given point (5, 6)

in the slope-point formula:

`\begin{gathered} y-y_1=m(x-x_1) \\ y-6=(5)/(4)(x-5) \end{gathered}`