Question

9b 9a) Use the slope formula to determine the rate of change eq y- and find the y-intercept "5" by substituting the x and y values into y=mx + b

Answer 1

A) We need to find the rate of change of the function first.

The rate of change or slope of the line is:

`m=\frac{y_2-y_1}{x_2-x_1_{}}`

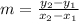
Where x and y are the coordinates of a point in line.

In order to calculate the slope we can take the poinst:

x1 = -6, y1 = 4

x2 = -2, y2= 1

Using the formula of above we find that the slope is:

`m=(1-4)/(-2-(-6))=-(3)/(4)`

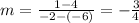
Now, in order to find the value of y-intercept of the line we can use formula:

`y=m\cdot x+b`

Which is the function of the line. From the formula of above we don't know the value of b (the y-intercept).

But we know that the formula must be valid for a point in the line. We can find the value of b replacing the coordinates of a point in the line, let's choose: x = -6 and y = 4, so:

`4=\text{ m}\cdot(-6)+b`

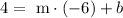
Now we use the value of m of above:

`4=(-(3)/(4))\cdot(-6)+b`

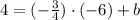
And from the last equation we can see that:

`b=4-(3)/(4)\cdot6=4-(9)/(2)=(8)/(2)-(9)/(2)=-(1)/(2)`

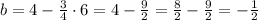
So, the equation of the line is:

`y\text{ = -}\frac{\text{3}}{4}\cdot x-(1)/(2)`

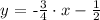
And the y-intercept is obtain replacing x = 0, so the y-intercept is: y = -1/2

b) From the stepts of above we already know an equation that represents the function! It is:

`y\text{ = -}\frac{\text{3}}{4}\cdot x-(1)/(2)`

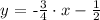
c) Now, we need to use the last equation to find y = n in the table. We know from the table that the value x for that value of y is x = 3, so we replace that value in the equation of the line:

`y\text{ = -}\frac{\text{3}}{4}\cdot3-(1)/(2)=-(9)/(4)-(1)/(2)=-(9)/(4)-(2)/(4)=-(11)/(4)`

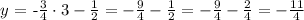
So the value of n is:

`n\text{ = -}\frac{\text{11}}{4}`