Question

Prove 2^n > n for all n equal to or greater than 1. I mostly need help with how to solve the problem when it is greater than rather than equal to. Thanks for the help

Answer 1

If
`n` is an integer, you can use induction. First show the inequality holds for
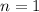
`n=1`. You have
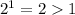
`2^1=2>1`, which is true.

Now assume this holds in general for
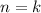
`n=k`, i.e. that
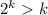
`2^k>k`. We want to prove the statement then must hold for
`n=k+1`.

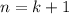
Because
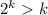
`2^k>k`, you have


`2^(k+1)=2*2^k>2k`

and this must be greater than
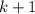
`k+1` for the statement to be true, so we require


`2k>k+1`

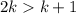
for
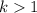
`k>1`. Well this is obviously true, because solving the inequality gives
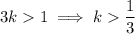
`3k>1\implies k>\frac13`. So you're done.

If you
`n` is any real number, you can use derivatives to show that
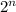
`2^n` increases monotonically and faster than
`n`.