Answer:
Using Cosine ratio:

As per the statement:
A ladder leaning against a wall makes an angle of 45º with the ground.
⇒Angle of elevation

It is also given that the length of the ladder is 20 feet.
Length of ladder = 20 feet.
We have to find the approximate distance of the foot of the ladder from the wall.
Let y be the distance of the foot of the ladder from the wall.
You can see the diagram as shown below in the attachment:
Hypotenuse side = Length of ladder = 20 feet
Adjacent side = Distance of foot of the ladder from the wall = y feet
Using cosine ratio we have;
Substitute the given values we have;

Multiply both sides by 20 we have;
⇒
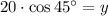
Simplify:
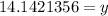
or
y = 14.1421356 feet
Therefore, the approximate distance of the foot of the ladder from the wall is, 14.14 feet