Answer:
40.83°
Explanation:
We are given that,
The horizontal distance between the two birds = 57.4 feet
The distance between the 2nd bird and the bird watcher = 49.6 feet
The given situation is represented by the following figure.
So, using the trigonometric form the angles in a right triangle, we have,
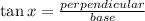
i.e.
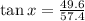
i.e.
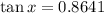
i.e.
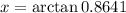
i.e. x= 40.83°
Hence, the angle of depression between the 1st bird and the bird watcher is 40.83°.