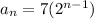Question

Write an explicit formula that represents the sequence defined by the following recursive formula: a1=7 and an=2a_n-1

Answer 1

`a_n=7(2^(n-1))`

Step-by-step explanation:

Given the sequence with the recursive formula:

`\begin{gathered} a_1=7 \\ a_n=2a_(n-1) \end{gathered}`

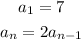
First, we determine the first three terms in the sequence.

`\begin{gathered} a_2=2a_(2-1)=2a_1=2*7=14 \\ a_3=2a_(3-1)=2a_2=2*14=28 \end{gathered}`

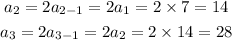
Therefore, the first three terms of the sequence are: 7, 14 and 28.

This is a geometric sequence where:

• The first term, a=7

,

• The common ratio, r =14/7 = 2

We use the formula for the nth term of a GP.

`\begin{gathered} a_n=ar^(n-1) \\ a_n=7*2^(n-1) \end{gathered}`

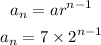
The explicit formula for the sequence is:

`a_n=7(2^(n-1))`