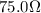Question

What is the equivalent resistance for a series circuit with three resistors: 19.2 ohms, 24.6 ohms, and 31.2 ohms?

Answer 1

the answer would be 75 ohms

Answer 2

Answer : The equivalent resistance for a series circuit is
`75.0\Omega`

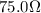
Explanation :

Equivalent resistance : It represents the total effect of all resistors in the circuit.

In series circuit, we add all the resistances of each component.

`R=R_1+R_2+R_3....`

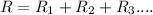
In parallel circuit, the reciprocal of the total resistance is equal to the sum of the reciprocals of the resistances of each component.

`(1)/(R)=(1)/(R_1)+(1)/(R_2)+(1)/(R_3)...`

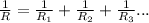
As we are given:

`R_1=19.2\Omega`

`R_2=24.6\Omega`

`R_3=31.2\Omega`

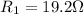
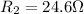
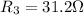
Now we have to calculate the equivalent resistance for a series circuit.

`R=R_1+R_2+R_3`

`R=19.2\Omega+24.6\Omega+31.2\Omega`

`R=75.0\Omega`

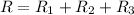
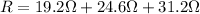
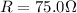
Therefore, the equivalent resistance for a series circuit is
`75.0\Omega`