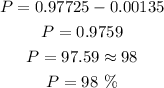Question

3. Suppose that the scores on a statewide standardized test are normally distributed with a mean of 69 and a standard deviation of 6. Estimate the percentage of scores that were(a) between 57 and 81. %(b) above 81. %(c) below 63. %(d) between 51 and 81. %

Answer 1

a) 95%

b) 2%

c) 16%

d) 98%

Step-by-step explanation:

We have the following:

This is a normal distribution

Mean = 69

Standard Deviation = 6

a) Between 57 and 81%

`\begin{gathered} z=(x-\mu)/(\sigma) \\ x=57 \\ z=(57-69)/(6)=-(12)/(6) \\ z=-2 \\ \\ x=81 \\ z=(81-69)/(6)=(12)/(6) \\ z=2 \\ \end{gathered}`

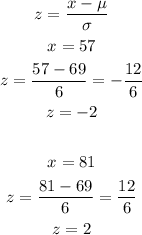
The probability that a score is between 57 & 81 is given by the Area between (z = -2) & (z = 2):

`\begin{gathered} P=0.97725-0.02275 \\ P=0.9545 \\ P=95.45\approx95 \\ P=95\text{ \%} \\ \\ \therefore P=95\text{ \%} \end{gathered}`

b) Above 81%

`\begin{gathered} z=(x-\mu)/(\sigma) \\ x>81 \\ z=(81-69)/(6) \\ z=(12)/(6)=2 \\ z=2 \end{gathered}`

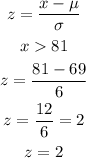
The probability that a score is above 81% is given by the area of the graph greater than (z = 2):

`\begin{gathered} P=0.02275 \\ P=2.275\approx2.3 \\ P=2.3\approx2 \\ P=2\text{ \%} \\ \\ \therefore P=2\text{ \%} \end{gathered}`

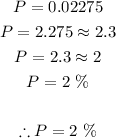
c) Below 63%

`\begin{gathered} x<63 \\ z=(63-69)/(6) \\ z=-(6)/(6)=-1 \\ z=-1 \end{gathered}`

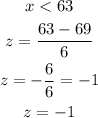
The probability that a score is below 63% is given by the area of the graph lesser than (z = -1):

`\begin{gathered} P=0.15866 \\ P=15.866\approx16 \\ P=16\text{ \%} \end{gathered}`

d) Between 51 and 81

`\begin{gathered} 51\le x\le81 \\ z=(51-69)/(6) \\ z=-(18)/(6)=-3 \\ z=-3 \\ \\ z=(81-69)/(6) \\ z=(12)/(6)=2 \\ z=2 \end{gathered}`

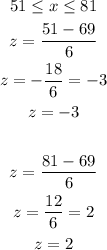
The probability that a score is between 51 & 81 is given by the Area between (z = -3 & (z = 2):

`\begin{gathered} P=0.97725-0.00135 \\ P=0.9759 \\ P=97.59\approx98 \\ P=98\text{ \%} \end{gathered}`