Question

if the author sells x Books per day his profit will be : J(X)= (-0.001x^2)+3x-1800Find the max profit per dayFind the amount of books the author must sell for the most profit

Answer 1

`\begin{gathered} \text{Given} \\ J(x)=\mleft(-0.001x^2\mright)+3x-1800 \end{gathered}`

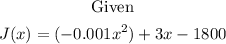
The given function in a quadratic function in standard form where

a = -0.001, b = 3, and c = -1800

It is a parabola that is facing downwards, therefore, the vertex of this parabola, (x,y) is the maximum of the function where

x is the amount of books that the author must sell for the most profit, and

y is the max profit per day.

We can find the vertex using

`x=(-b)/(2a)`

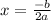
Substitute the following values, and we get

`\begin{gathered} x=(-b)/(2a) \\ x=(-3)/(2(-0.001)) \\ x=(-3)/(-0.002) \\ x=1500 \end{gathered}`

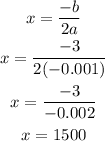
Now that we have x, plug it in the original function to solve for y

`\begin{gathered} J(x)=\mleft(-0.001x^2\mright)+3x-1800 \\ J(1500)=-0.001(1500)^2_{}+3(1500)-1800 \\ J(1500)=-2250+4500-1800 \\ J(1500)=450 \end{gathered}`

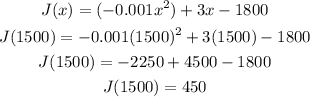
We have determine that the vertex of the function is at (1500,450). We can now conclude that

The max profit per day is $450.

The amount of of books the author must sell for the most profit is 1500 books.