Question

(D^2 - 1) y = x^2 sinx

Answer 1

`(D^2-1)y=x^2\sin x`

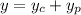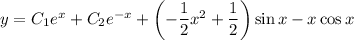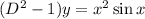
First consider the homogeneous part,


`(D^2-1)y=(\mathrm d^2y)/(\mathrm dx^2)-y=0`

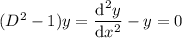
which has characteristic equation


`r^2-1=(r-1)(r+1)=0`

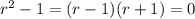
This has roots
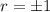
`r=\pm1`, so the characteristic solution is


`y_c=C_1e^x+C_2e^(-x)`

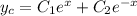
For the nonhomogeneous part, consider a solution of the form


`y_p=(a_2x^2+a_1x+a_0)\sin x+(b_2x^2+b_1x+b_0)\cos x`

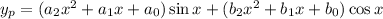
which has second derivative


`(\mathrm d^2y_p)/(\mathrm dx^2)=(-b_2x^2+(4a_2x-b_1)x+2a_1-b_0+2b_2)\cos x+(a_2x^2+(a_1+4b_2)x+a_0-2a_2+2b_1)\sin x`

Substituting into the ODE gives


`(-2b_2x^2+(4a_2-2b_1)x+2a_1-2b_0+2b_2)\cos x+(-2a_2x^2+(-2a_2-4b_2)x-2a_0-2b_1+2a_2)\sin x=x^2\sin x`

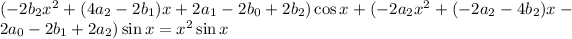
Matching up coefficients gives the system


`\begin{cases}-2b_2=0\\4a_2-2b_1=0\\2a_1-2b_0+2b_2=0\\-2a_2=1\\-2a_1-4b_2=0\\-2a_0-2b_1+2a_2=0\end{cases}`

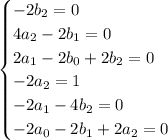
which has solutions


`a_2=-\frac12,a_1=0,a_0=\frac12,b_2=0,b_1=-1,b_0=0`

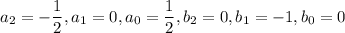
So the particular solution is


`y_p=\left(-\frac12x^2+\frac12\right)\sin x-x\cos x`

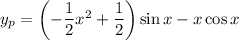
Therefore the general solution is


`y=y_c+y_p`

`y=C_1e^x+C_2e^(-x)+\left(-\frac12x^2+\frac12\right)\sin x-x\cos x`