Given:
Speed of current (y)= 6 km/hour
Distance = d km
Speed of boat in still water = x km/hour
Speed of the cruiser with the current= (x+6) km/hour
Speed of the cruiser against the current= (x-6) km/hour
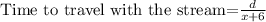

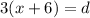

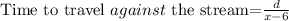
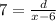
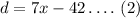
From equation (1) and (2)
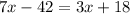
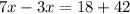

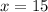
Therefore the speed of the without a current is 15km/hour.