Answer:
1) The factorized form of the polynomial is
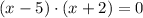 .
.
2) The factorized form of the polynomial is
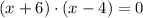 .
.
3)
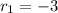 ,
,
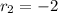 . (Option D)
. (Option D)
4)
 ,
,
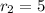 . (Option A)
. (Option A)
Explanation:
All exercise are case of factorization of second grade polynomials of the form
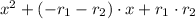 , where
, where
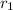 and
and
 are the two roots of the polynomial. Now we proceed to solve each polynomial:
are the two roots of the polynomial. Now we proceed to solve each polynomial:
1)

In this case, the coefficients have the following characteristics:

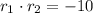
The solution of this system of nonlinear equations is:
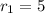 ,
,
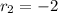 .
.
Then, the factorized form of the polynomial is:
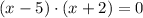
2)
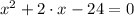
In this case, the coefficients have the following characteristics:
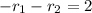
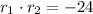
The solution of this system of nonlinear equations is:
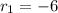 ,
,
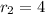 .
.
Then, the factorized form of the polynomial is:
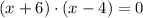
3)
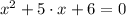
In this case, the coefficients have the following characteristics:
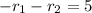
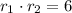
The solution of this system of nonlinear equations is:
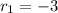 ,
,
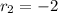 .
.
Hence, the correct answer is D.
4)
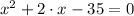
In this case, the coefficients have the following characteristics:
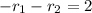
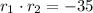
The solution of this system of nonlinear equations is:
 ,
,
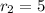 .
.
Hence, the correct answer is A.