Answer:
The amount that should be invested is $1621.16
Step-by-step explanation:
The formula for continuous compound interest is:
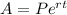
Where:
A is the amount of money after t years
P is the invested amount (what we want to find, in this case)
r is the rate of compounding in decimal
t i the amount of time compounding, in years
Then, in this case:
A = $2000
r = 0.07 (to convert percentage to decimal, we divide by 100: 7% / 100 = 0.07)
t = 3 years
Then:
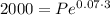
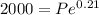
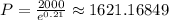
To the nearest cent, P = $1621.16