
those are the vertex form of a parabola... so hmmm
the vertex of this one is at 0,1 and intercepts or "solutions" are at -1 and 1, so is opening downwards, notice the picture below
that means, the squared variable is the "x", thus the form is
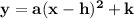
now, we know the vertex is at 0,1, and two x-intercepts of
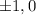
thus

solve for "a", to see what that coefficient is, then plug it back in the vertex form equation