Question

Use the formula for the probability of the complement of an event.A single card is drawn from a deck. What is the probability of not drawing a 7?

Answer 1

occur

the answer is 12/13 or 0.932

Step-by-step explanation

when you have an event A, the complement of A, denoted by.

`A^(-1)`

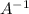
consists of all the outcomes in wich the event A does NOT ocurr

it is given by:

`P(A^(-1))=1-P(A)`

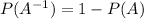
Step 1

find the probability of event A :(P(A)

The probability of an event is the number of favorable outcomes divided by the total number of outcomes possible

`P=\frac{favorable\text{ outcomes}}{\text{total outcomes}}`

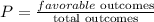
so

let

favorable outcome = 4 (there are four 7 in the deck)

total outcomes=52

hence,replacing

`\begin{gathered} P=(4)/(52)=(1)/(13) \\ P(A)=(1)/(13) \end{gathered}`

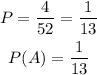
Step 2

now, to find the probability that the event does NOT ocurrs ( not drawing a 7)

let's apply the formula

`P(A^(-1))=1-P(A)`

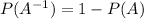
replace

`\begin{gathered} P(A^(-1))=1-(1)/(13) \\ P(A^(-1))=(13-1)/(13)=(12)/(13) \\ P(A^(-1))=0.923 \end{gathered}`

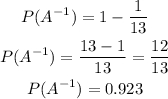
therefore, the answer is 12/13 or 0.932

I hope this helps you