Question

Recall that for use of a normal distribution as an approximation to the binomial distribution, the conditions np greater than or equal to 5 and nq greater than or equal to 5 must be met. For p= 0.9, compute the minimum sample size needed for use of the normal approximation. Round your answer to the next whole number.

The minimum sample size needed for use of the normal approximation is =

Answer 1

The minimum sample size needed for use of the normal approximation is 50.

Explanation:

Suitability of the normal distribution:

In a binomial distribution with parameters n and p, the normal approximation is suitable is:

np >= 5

n(1-p) >= 5

In this question, we have that:

p = 0.9

Since p > 0.5, it means that np > n(1-p). So we have that:

`n(1-p) \geq 5`

`n(1 - 0.9) \geq 5`

`0.1n \geq 5`

`n \geq (5)/(0.1)`

`n \geq 50`

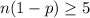
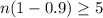
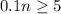
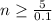
The minimum sample size needed for use of the normal approximation is 50.