Question

Calculate Sy for the arithmetic sequence in which ag = 17 and the common difference is d =-21.O A -46O B.-29.2O C. 32.7O D. 71.3

Answer 1

Given: An arithmetic sequaence has the following parameters

`\begin{gathered} a_9=17 \\ d=-2.1 \end{gathered}`

To Determine: The sum of the first 31st term.

Please note that the sum of the first 31st term is represented as

`S_(31)=\text{ sum of the first 31st term}`

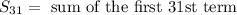
The formula for the finding the n-term of an arithmetic sequence (AP) is

`\begin{gathered} a_n=a+(n-1)d \\ \text{Where} \\ a_n=n-\text{term} \\ a=\text{first term} \\ d=\text{common difference} \end{gathered}`

Since, we are given the 9th term as 17, we can calculate the first term a, as shown below:

`\begin{gathered} a_9=17 \\ \text{Substituting into the formula} \\ a_9=a+(9-1)d \\ a_9=a+8d \\ \text{Therefore:} \\ a+8d=17 \\ d=-2.1 \\ a+8(-2.1)=17 \\ a-16.8=17 \\ a=17+16.8 \\ a=33.8 \end{gathered}`

Calculate the sum of the first 31st term.

The formula for finding the first n-terms of an arithmetic series is given as

`S_n=(n)/(2)(2a+(n-1)d)`

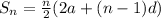
We are given the following:

`a=33.8,n=31,d=-2.1`

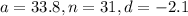
Substitute the given into the formula:

`\begin{gathered} S_(31)=(31)/(2)(2(33.8)+(31-1)-2.1) \\ S_(31)=15.5(67.6)+(30)-2.1) \\ S_(31)=15.5(67.6-63) \end{gathered}`
`\begin{gathered} S_(31)=15.5(4.6) \\ S_(31)=71.3 \end{gathered}`

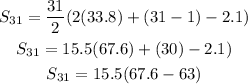
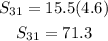
Hence, the sum of the first 31st term of the A.P is 71.3, OPTION D