A random variable

following a binomial distribution with success probability
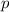
across

trials has PMF
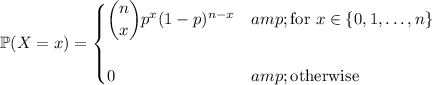
where
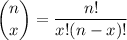
.
The mean of the distribution is given by the expected value which is defined by
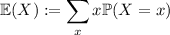
where the summation is carried out over the support of

. So the mean is
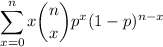
Because this is a proper distribution, you have
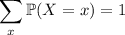
which is a fact that will be used to evaluate the sum above.
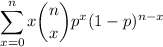

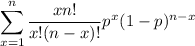
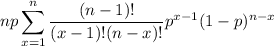
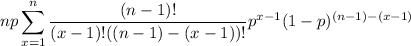
Letting
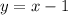
, this becomes
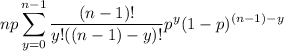
Observe that the remaining sum corresponds to the PMF of a new random variable

which also follows a binomial distribution with success probability
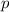
, but this time across

trials. Therefore the sum evaluates to 1, and you're left with
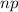
as the expression for the mean for

.