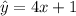Question

Given the data points (1,5), (3,13) and (5,21), which of the following equations describes the best-fit line?

y-hat=4+1x
y-hat=2+4x
y-hat=1+4x
y-hat=-1+4x

Answer 1

We're looking for a line of best fit of the form
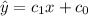
`\hat y=c_1x+c_0`. Set up a matrix equation:


`\begin{bmatrix}1&1\\3&1\\5&1\end{bmatrix}\begin{bmatrix}c_1\\c_0\end{bmatrix}=\begin{bmatrix}5\\13\\21\end{bmatrix}`

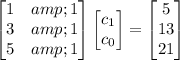
Multiply both sides on the left by the transpose of the coefficient matrix:


`\begin{bmatrix}1&3&5\\1&1&1\end{bmatrix}\begin{bmatrix}1&1\\3&1\\5&1\end{bmatrix}\begin{bmatrix}c_1\\c_0\end{bmatrix}=\begin{bmatrix}1&3&5\\1&1&1\end{bmatrix}\begin{bmatrix}5\\13\\21\end{bmatrix}`

`\begin{bmatrix}35&9\\9&3\end{bmatrix}\begin{bmatrix}c_1\\c_0\end{bmatrix}=\begin{bmatrix}149\\39\end{bmatrix}`

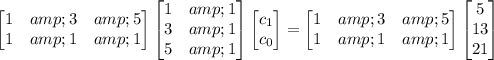
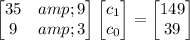
Multiply both sides by the inverse of the new coefficient matrix:


`\begin{bmatrix}35&9\\9&3\end{bmatrix}^(-1)\begin{bmatrix}35&9\\9&3\end{bmatrix}\begin{bmatrix}c_1\\c_0\end{bmatrix}=\begin{bmatrix}35&9\\9&3\end{bmatrix}^(-1)\begin{bmatrix}149\\39\end{bmatrix}`

`\begin{bmatrix}c_1\\c_0\end{bmatrix}=\begin{bmatrix}4\\1\end{bmatrix}`

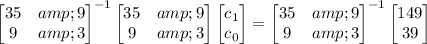
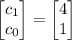
So we end up with a best-fit line of


`\hat y=4x+1`