Given:
The equation is
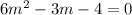
To find:
The number and types of solutions for the given equation.
Solution:
We have,
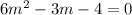
It is a 2nd degree polynomial because the highest degree of the variable x is 2.
Number of solutions = Degree of the polynomial
Number of solutions = 2
Therefore, the given equation has 2 solutions.
In a quadratic equation
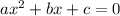 , if
, if
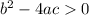 , then the equation has two distinct real solutions.
, then the equation has two distinct real solutions.
For the given equation, a=6, b=-3 and c=-4.
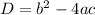
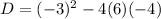
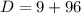
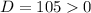
Therefore, the given equation has two distinct real solutions.