Usually, to calculate the area of a solid we need to calculate the area of every face. Here we have a rectangle down, and four triangles. Our desired area (TA) will be the sum of those areas. Let's calculate those areas:
Area of the rectangle) The area of the rectangle (R) is
![R=(leng\ldots)(wid\ldots)=(10cm)\cdot(4cm)=40\operatorname{cm}^2]()
Area of the front triangle and the back tringle) Note that the front triangle and the back triangle are the "same". So the area of each of them is equal (this simplifies our work...). The area of each of them (FB) is
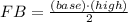
What is their high?
The triangle with red, blue, and green edges is a right triangle... Its hypotenuse is the blue edge. We know the red edge, its length is 6cm, but what is the length of the green edge? Because our solid is a rectangular pyramid, we can say that the green edge is half of the length of the rectangle. that is, 5cm (10cm/2). Now, we know the red and green edges; so we can apply The Pythagoras theorem to get
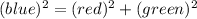
![(blue)^2=(6cm)^2+(5cm)2=36\operatorname{cm}+25\operatorname{cm}=61\operatorname{cm}^2]()
![undefined]()