Question

In a study of 205 adults, the mean heart rate was 75 beats per minute. Assume the population of heart rates is known to be approximately normal with a standard deviation of 8 beats per minute. What is the 95% confidence interval for the mean beats per minute?

A. 73.9 − 76.1
B. 73.7 − 76.1
C. 73.9 − 76.3
D. 70.9 − 73.3

Answer 1

I believe that the answer is A. :) Hope this helps!

Answer 2

73.9-76.1

Explanation:

Given :
`\bar{x} = 75`

`\sigma = 8`

`n = 205`

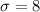
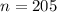
To Find: What is the 95% confidence interval for the mean beats per minute?

Solution:

Formula :
`\bar{x}\pm z(\sigma)/(√(n))`

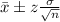
z = 1.96 at 95% confidence interval

Substitute the values in the formula:

`75 \pm 1.96(8)/(√(205))`

`75 -1.96(8)/(√(205)),75 0+1.96(8)/(√(205))`

`73.9,76.1`

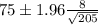
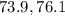
Hence the 95% confidence interval for the mean beats per minute is 73.9-76.1

Thus Option A is true.