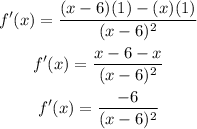Question

Use the Quotient Rule to find the derivative of the function.f(x) = x/(x − 6)f'(x)=

Answer 1

`(-6)/((x-6)^2)`

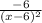
Step-by-step explanation

We want to find the derivative of the function:

`f(x)=(x)/(x-6)`

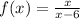
The quotient rule states that:

`f^(\prime)(x)=(v(du)/(dx)-u(dv)/(dx))/(v^2)`

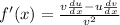
where u = the numerator of the function

v = the denominator of the function

From the function, we have that:

`\begin{gathered} u=x \\ v=x-6 \end{gathered}`

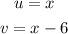
Now, we have to differentiate both u and v:

`\begin{gathered} (du)/(dx)=1 \\ (dv)/(dx)=1 \end{gathered}`

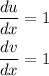
Therefore, the derivative of the function is:

`\begin{gathered} f^(\prime)(x)=((x-6)(1)-(x)(1))/((x-6)^2) \\ f^(\prime)(x)=(x-6-x)/((x-6)^2) \\ f^(\prime)(x)=(-6)/((x-6)^2) \end{gathered}`