Answer:
The area of the shaded part is:
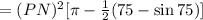
Step-by-step explanation:
The area of the shaded part is the subtraction of the area of the unshaded part from the area of the whole circle.
Area of the ushaded part is:
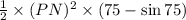
Area of the circle is:
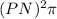
Area of the shaded part is:
