Question

The diamond method for factoring: Fill in the missing value

Answer 1

Consider a quadratic expression, let "m" and "n" represent the factors.

The diamond method of factoring is the following:

On the left of the diamond, there is one of the factors, for example, "m", of the right of the diamond you will find the other factor "n".

On the top of the diamond, you will find the product of both factors, on the bottom of the diamond you will find the sum of the factors.

Looking at the given diamond, you know the result of the product and the sum of both factors:

`m*n=-15`
`m+n=14`

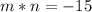
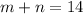
Using these expressions, you can find both factors.

- First, write the second expression for one of the variables, for example, for "n"

`\begin{gathered} m+n=14 \\ m=14-n \end{gathered}`

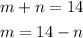
- Second, replace the expression obtained on the second equation:

`\begin{gathered} m*n=-15 \\ (14-n)n=-15 \end{gathered}`

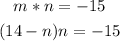
Distribute the multiplication

`14n-n^2=-15`

Zero the expression and order the terms from greatest to least:

`\begin{gathered} 14n-n^2+15=-15+15 \\ 14n-n^2+15=0 \\ -n^2+14n+15=0 \end{gathered}`

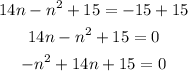
- Third, use the quadratic expression to determine the possible values of n:

`x=(-b\pm√(b^2-4ac))/(2a)`

Where

a is the coefficient of the quadratic term

b is the coefficient of the x-term

c is the constant

For the quadratic expression obtained, where "n" represents the x-variable.

`-n^2+14n+15=0`

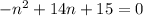
The coefficients are:

a= -1

b=14

c=15

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ n=(-14\pm√(14^2-4*(-1)*15))/(2*(-1)) \\ n=(-14\pm√(196+60))/(-2) \\ n=(-14\pm√(256))/(-2) \\ n=(-14\pm16)/(-2) \end{gathered}`

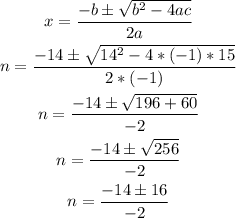
Solve the sum and difference separately to determine both possible values for "n"

→Sum:

`\begin{gathered} n=(-14+16)/(-2) \\ n=(2)/(-2) \\ n=-1 \end{gathered}`

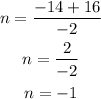
→Difference:

`\begin{gathered} n=(-14-16)/(-2) \\ n=(-30)/(-2) \\ n=15 \end{gathered}`

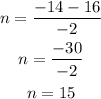
- Finally, determine the possible value/s of m:

For n=-1

`\begin{gathered} m+n=14 \\ m+(-1)=14 \\ m-1=14 \\ m=14+1 \\ m=15 \end{gathered}`

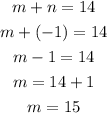
For n=15

`\begin{gathered} m+n=14 \\ m+15=14 \\ m=14-15 \\ m=-1 \end{gathered}`

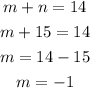
So, the factors are -1 and 15 and the diamond is: