Question

What are the zeros of the function?
f(t)=t^2-13t+36

Answer 1

To find zeroes of the equation solve the equation
t^2-13t+36
=t^2-(9+4)t+36
=t^2-9t-4t+36
=t(t-9)-4(t-9)
=(t-9)(t-4)
So zeroes are 9 and 4

Answer 2

the zeros of the function are: 9 and 4

Explanation:

Given the function:

`f(t) = t^2-13t+36`

To find the zeros of the function:

Set f(t) = 0

then;

`t^2-13t+36 = 0`

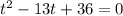
Split the middle term as: -9 and -4 we have;

`t^2-9t-4t+36 = 0`

⇒
`t(t-9)-4(t-9) = 0`

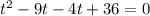
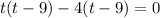
Take (t-9) common we have;

`(t-9)(t-4) = 0`

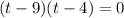
By zero product property we have;

t-9 = 0 and t-4 = 0

⇒t = 9 and t = 4

Therefore, the zeros of the function are: 9 and 4