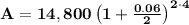Question

14,800 at 6% compounded semiannually for 4 years.. I need to know the interest and the compound amount

Answer 1

`\bf \qquad \textit{Compound Interest Earned Amount} \\\\ A=P\left(1+(r)/(n)\right)^(nt) \quad \begin{cases} A=\textit{compounded amount}\\ P= \begin{array}{llll} \textit{original amount}\\ \textit{deposited} \end{array}\to &\$14,800\\ r=rate\to 6\%\to (6)/(100)\to &0.06\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{semi-annually, meaning twice} \end{array}\to &2\\ t=years\to &4 \end{cases}`

now, that will give you "A", or the compounded amount

what's the interest earned? well, subtract the original amount, the Principal, from A, A - P, and you'd be left with the earned interest

--------------------------------------------------------------------------------------------

`\bf A=14,800\left(1+(0.06)/(2)\right)^(2\cdot 4)`