Question

Determine if each expression is equivalent to
`\frac{ {7}^(6) }{ {7}^(3) }`

Answer 1

The question says we are to check the options that are equal

`(7^6)/(7^3)`

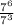
Using the law of indices

`(7^6)/(7^3)=7^{6-3\text{ }}=7^3`

So we will check all the options(applying the laws of indices)

The first option is

`7^9(7^(-6))=7^(9-6)=7^3`

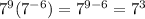
yes, the first option is equivalent

We will move on and check the second option

`(7^(-8))/(7^(-11))\text{ = }7^(-8+11)=7^3`

Yes the second option is equivalent

We will move on to check the third option

`(7^5)(7^3)divideby7^{4\text{ }}=7^{5+3-4\text{ }}=7^4`

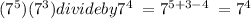
No the third option is not eqquivalent to the question

We will move to tthe next option, fourth option

`7^{-3\text{ }}*7^{6\text{ }}=7^(-3+6)=7^3`

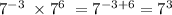
yes this option is equivalent to the fraction

Moving on to the fifth option

`(7^3)^{0\text{ }}=7^(3*0)=7^0=\text{ 1}`

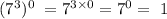
No the fifth option is not equivalent to the question