Question

The table of values represents a quadratic function.What is the average rate of change for f(x) from x=−10 to x = 0?Please help me with this problem so that my son can understand better. Enter your answer in the box.xf(x)−10184−5390−654910204

Answer 1

We are given a quadratic function and the rather than the equation for this function we already have the outputs at each given input as shown in the table provided. This means, for example, for the function given, when the input is -10, the output is 184. Thus the table includes among other values;

`x=-10|f(x)=184`

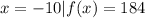
To calculate the average rate of change we shall apply the formula for the slope (which is also the average rate of change). This is given below;

`\text{Aerage Rate of Change}=(f(b)-f(a))/(b-a)`

Note that the variables are;

The first input value is -10 and the function at that value is 184

The second input value is 0 and the function at that value is -6

We now have;

`\begin{gathered} a=-10,f(a)=184 \\ b=0,f(b)=-6 \end{gathered}`

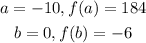
We can now substitute these into the formula shown nearlier and we'll have;

`\begin{gathered} \text{Ave Rate Of Change}=(f(b)-f(a))/(b-a) \\ =(-6-184)/(0-\lbrack-10\rbrack) \end{gathered}`
`\begin{gathered} =(-190)/(0+10) \\ \end{gathered}`
`=(-190)/(10)`
`\text{Average Rate of Change}=-19`

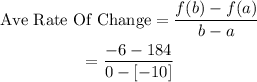
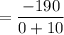
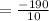
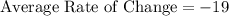
ANSWER:

The average rate of change over the given interval is -19