Answer:
The equation in slope-intercept form is:
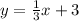
So the second option is the correct one.
Explanation:
Step 1: Identify the gradient
The perpendicular line's equation is given as:
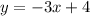
This equation is in the form of:

Upon comparing the
 components of both equations, we get
components of both equations, we get
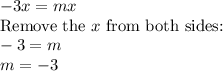
So, the gradient of this 'reference' equation is -3.
The equation we need to find is perpendicular to this 'reference' equation.
So, its gradient should be the negative reciprocal of the gradient of the 'reference' equation.
The negative reciprocal of -3 is:

So, the gradient of our equation is
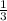 .
.
Step 2: Create the equation:
The equation crosses the x-axis at -9, which means its y-coordinate is 0 (at x-axis, y=0) ,so its coordinate is
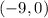 .
.
The formula for an equation is:
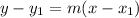
The coordinate
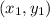 is
is
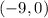 , and the gradient (
, and the gradient (
 ) is
) is
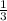 .
.
Substitute the values into the equation:
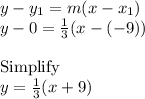
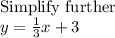
Since, the slope-intercept form is:

We already have our equation in the slope-intercept form.